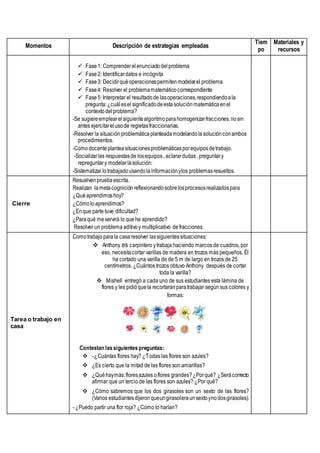
La sesión de aprendizaje tuvo como objetivo enseñar a los estudiantes a resolver problemas aditivos y multiplicativos con fracciones. La sesión comenzó con una actividad de motivación que presentó un problema sobre fracciones. Luego, los estudiantes trabajaron en equipos usando estrategias como identificar datos e incógnitas para modelar problemas y resolverlos. Al final, los estudiantes reflexionaron sobre lo aprendido y recibieron una tarea sobre fracciones para completar en casa.

1. SESIÓN DE APRENDIZAJE 5° “B” ( aula virtual)
Nombre del docente: Asunciona Virgilia Tello Santos
TÍTULO DELASESIÓN PROBLEMASADITIVOS y MULTIPLICATIVOSCONFRACCIONES.
INTENCIÓNDEL APRENDIZAJE Resuelve problemasaditivos y Multiplicativos confracciones.
APRENDIZAJES ESPERADOS
Competencia Capacidades Indicadores
Inst. de
evaluación
. Actúa y piensa
matemáticamente
en situacionesde
cantidad.
Matematiza
situaciones.
Plantearelacionesentrelosdatos enproblemasdecambio,
expresándolosenunmodelodesoluciónaditiva(adición) ymultiplicativa
(multiplicación) confracciones.
Prueba
objetiva.
Elaboray usa
estrategias.
Empleaestrategiasheurísticasoprocedimientosparasumaralresolver
problemasconfraccionesheterogéneas.
SECUENCIA DIDÁCTICA DE LA SESIÓN
Momentos Descripción de estrategias empleadas
Tiem
po
Materiales y
recursos
Inicio
Motivaci
ón
Plantearla siguientesituaciónproblemática:
Sofía ha recogido12naranjasenunacanastay ha separado1/3de esas
naranjaspararegalarlasasu primoJason.¿Cómoencontraremos1/3de 12?
¿Cómorepresentaremos1/3de cadagrupoen las tarjetas?
Todos respondenquehay4. Ladocenteprecisa que1/3 de 12 es 4 y se
escribe así: 1/3 de 12=4
Regletascon
fracciones
Papelotes
Cuadernodel
área
Plumones.
Saberes
previos
Recuperarsaberespreviosa partir delas siguientespreguntas ¿Unanaranja
partidoen dos partescomosellama?¿Cómorepresentamos1/3decada
grupoen las tarjetas? ¿Quétipode fraccionesseusanenel problema?
-
Conflicto
cognitivo
Plantearel siguienteconflictocognitivo:¿Quéprocesossiguespararesolverel
problema.
-
Propósit
o
didáctico
Presentar elpropósitode la sesión:En esta sesiónaprenderása relacionarlos
datos conunmodelodesoluciónaditiva.
Desarrollo
Los estudiantesporequiposresuelvenla situaciónproblemáticapropuesta.
Socializarlasrespuestas, los equiposquelohagancorrectamentedeberán
explicarelprocesodesarrollado.
Usandoel pasode polya
* Unaestrategia generalderesolucióndeproblemas,incluyelassiguientes
fases:

2. Momentos Descripción de estrategias empleadas
Tiem
po
Materiales y
recursos
 Fase1: Comprenderelenunciadodelproblema
 Fase2: Identificardatos e incógnita
 Fase3: Decidirquéoperacionespermitenmodelarel problema
 Fase4: Resolver el problemamatemáticocorrespondiente
 Fase5: Interpretar el resultadode lasoperaciones,respondiendoala
pregunta:¿cuálesel significadodeestasoluciónmatemáticaenel
contextodelproblema?
-Se sugiereemplearelsiguientealgoritmoparahomogenizarfracciones,nosin
antes ejercitarelusode regletasfraccionarias.
-Resolver la situaciónproblemáticaplanteadamodelandolasoluciónconambos
procedimientos.
-Comodocenteplanteasituacionesproblemáticasporequiposdetrabajo.
-Socializarlas respuestasde losequipos, aclarardudas, preguntary
repreguntary modelarlasolución:
-Sistematizar lotrabajadousandolainformaciónylos problemasresueltos.
Cierre
Resuelvenpruebaescrita.
Realizan la metacognición reflexionandosobrelosprocesosrealizadospara
¿Quéaprendimoshoy?
¿Cómolo aprendimos?
¿Enque parte tuve dificultad?
¿Paraqué meservirá lo quehe aprendido?
Resolver un problema aditivoy multiplicativo defracciones.
Tarea o trabajo en
casa
Comotrabajoparala casaresolver lassiguientessituaciones:
 Anthony es carpintero ytrabaja haciendo marcos de cuadros, por
eso, necesitacortar varillas de madera en trozos más pequeños. Él
ha cortado una varilla de de 5 m de largo en trozos de 25
centímetros. ¿Cuántos trozos obtuvo Anthony después de cortar
toda la varilla?
 Mishell entregó a cada uno de sus estudiantes esta lámina de
flores y les pidióquela recortaranparatrabajar según sus colores y
formas:
Contestan lassiguientespreguntas:
 -¿Cuántas flores hay? ¿Todas las flores son azules?
 ¿Es cierto que la mitad de las flores son amarillas?
 ¿Quéhaymás:floresazules oflores grandes?¿Porqué? ¿Serácorrecto
afirmar que un tercio de las flores son azules? ¿Por qué?
 ¿Cómo sabremos que los dos girasoles son un sexto de las flores?
(Varios estudiantesdijeronqueungirasoleraunsextoynodosgirasoles).
- ¿Puedo partir una flor roja? ¿Cómo lo harían?

3. Momentos Descripción de estrategias empleadas
Tiem
po
Materiales y
recursos
, ¿qué propondrían para ayudar a Nathalia? ¿Trabajarían con las doce flores?
¿Por qué?
Fichade aplicación
Fotografíasensesiónde aprendizaje
Presentación de material concreto Observación de material
Los alumnos estánelaborandosumaterial Elaboransu material porequipo

4. TelloSantos_AsuncionaVirgilia_Grupo2_Aula4
Trabajo enequipoporlosalumnos
Exposiciónde trabajosrealizadosporequipo
Graficandofraccionesporequipo
Sistematizandolainformaciónconlos
estudiantes