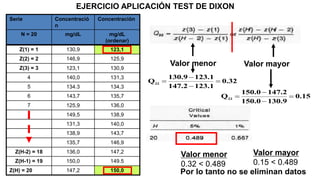
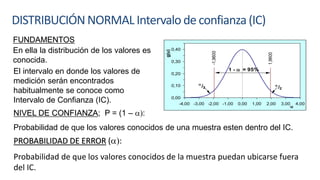
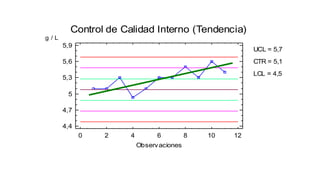
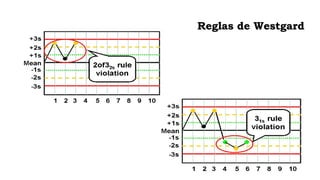
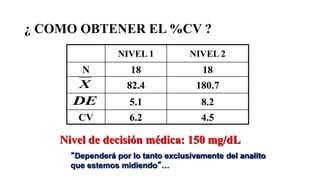
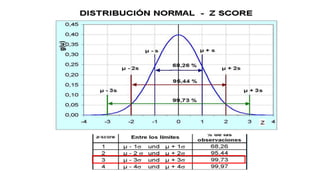
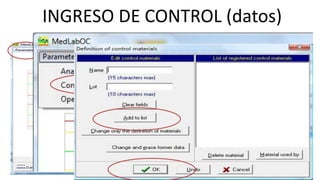
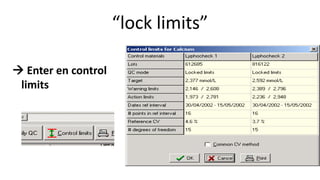
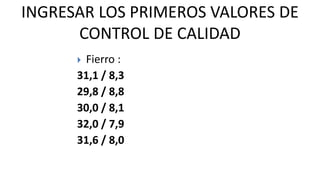
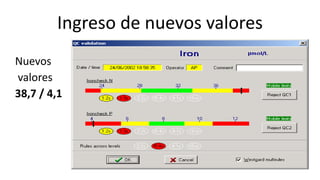
Este documento describe los procedimientos de control de calidad interno de un laboratorio clínico. Explica cómo construir gráficas de control y aplicar reglas estadísticas como las de Westgard para identificar errores sistemáticos y aleatorios. También cubre la importancia de la participación en programas de control de calidad externo y cómo evaluar la competencia analítica del laboratorio mediante el cálculo del error total.

1. Control de Calidad Interno
Yerko Bravo

2. Control de Calidad Interno GP 1.3 – APL 1.3

3. ASEGURAMIENTO DE LA CALIDAD
PROCESO ANALÍTICO
Cumple
CCI
Material
Control
Corrida Analítica Gráficas
Levey-Jennings Reglas de
Westgard
Error Total - Cartas OPSpecs – Nº Sigma -
ΔSEcrit (inexactitud e imprecisión del método)Cumple
No
Si
Material Control
con trazabilidad
No Si Aseguramiento
de la calidad de
Resultados y
Procedimiento
Acciones Preventivas
y Correctivas
CCE
Material
Control

5. GRÁFICAS DE LEVEY-JENNINGS

7. CONTROL NIVEL 1
GRAFICAS DE LEVEY
JENNINGS
N = 20 Datos
82 82
76 77
85 81
77 75
78 86
87 82
78 83
83 75
76 87
84 77

8. N = 20 Datos
190 176
185 185
178 170
186 194
174 181
177 175
185 170
183 182
169 169
164 178
CONTROL NIVEL 2
GRAFICAS DE LEVEY
JENNINGS

9. CRITERIOS PARA ELIMINAR
DATOS EXTREMOS
• Test de Dixon

10. Serie Concentració
n
Concentración
N = 20 mg/dL mg/dL
(ordenar)
Z(1) = 1 130,9 123,1
Z(2) = 2 146,9 125,9
Z(3) = 3 123,1 130,9
4 140,0 131,3
5 134.3 134,3
6 143,7 135,7
7 125,9 136,0
149,5 138,9
131,3 140,0
138,9 143,7
135,7 146,9
Z(H-2) = 18 136,0 147,2
Z(H-1) = 19 150,0 149.5
Z(H) = 20 147,2 150,0
EJERCICIO APLICACIÓN TEST DE DIXON
Valor menor Valor mayor
0.32
123.1147.2
123.1130.9
Q22 



0.15
130.9150.0
147.2150.0
Q22 



Valor menor
0.32 < 0.489
Valor mayor
0.15 < 0.489
Por lo tanto no se eliminan datos

11. N = 20 Datos
82 82
76 77
85 81
77 75
78 86
87 82
78 83
83 75
76 87
84 77
80.6
4.1
8.2
12.3
PARAMETROS ESTADISTICOS
X
DE
2DE
3DE
CONTROL NIVEL 1 GRAFICAS DE LEVEY
JENNINGS

12. N = 20 Datos
190 176
185 185
178 170
186 194
174 181
177 175
185 170
183 182
169 169
164 178
178.6
7.9
15.8
23.7
PARAMETROS ESTADISTICOS
X
DE
2DE
3DE
CONTROL NIVEL 2 GRAFICAS DE LEVEY
JENNINGS

13. ¿COMO CONSTRUIR GRAFICAS DE LEVEY
JENNINGS?

14. FUNDAMENTOS
En ella la distribución de los valores es
conocida.
El intervalo en donde los valores de
medición serán encontrados
habitualmente se conoce como
Intervalo de Confianza (IC).
-1,9600
1,9600
0,00
0,10
0,20
0,30
0,40
-4,00 -3,00 -2,00 -1,00 0,00 1,00 2,00 3,00 4,00
u
g(u)
1 - a = 95%
a
/2
a
/2
PROBABILIDAD DE ERROR (a):
Probabilidad de que los valores conocidos de la muestra puedan ubicarse fuera
del IC.
NIVEL DE CONFIANZA; P = (1 – a):
Probabilidad de que los valores conocidos de una muestra esten dentro del IC.
DISTRIBUCIÓNNORMALIntervalo de confianza(IC)

15. DISTRIBUCIÓNNORMAL – CARTA CONTROL

16. DATOS A GRAFICAR

17. DATOS A GRAFICAR

19. ERROR SISTEMATICO
ERROR ALEATORIO
REGLAS DE WESTGARD

20. ERROR SISTEMÁTICO (ES) y CCI
Un error sistemático se manifiesta como un
cambio en la media de los valores de control.
El cambio en la media puede ser gradual y
mostrarse como una tendencia o como un
desplazamiento.

21. Control de Calidad Interno (Tendencia)
Observaciones
g / L
CTR = 5,1
UCL = 5,7
LCL = 4,5
0 2 4 6 8 10 12
4,4
4,7
5
5,3
5,6
5,9

22. ERROR SISTEMÁTICO y CCI
Deterioro de la fuente de luz del instrumento
Acumulación gradual de desechos en la tubería
Envejecimiento de los reactivos
Deterioro gradual de la integridad del filtro de luz
Las posibles causas de una tendencia puede
incluir:

23. Control de Calidad Interno (Desplazamiento)
Observaciones
mg / dL
CTR = 80,0
UCL = 110,0
LCL = 50,0
0 2 4 6 8 10 12
50
60
70
80
90
100
110
120

24. ERROR SISTEMÁTICO y CCI
Falla o cambio repentino en la fuente de luz
Cambio de lote del reactivo
Cambio en la temperatura o humedad ambiental
Falla del sistema de muestreo
Las posibles causas de los desplazamientos
puede incluir:

25. Expresable en: unidades de la magnitud medida
Concepto relacionado de forma directa: sesgo
(bias), veracidad
Estimación cuantitativa: inexactitud
Aplicables a: una medida, media de un grupo de
medidas, un procedimiento de medida, un
instrumento
ERROR SISTEMATICO

26. ERROR SISTEMATICO
Causas del error sistemático:
Calibración incorrecta: afecta a todas las muestras. Debe ser evitado
o corregido.
Inespecificidad (metrológica): afecta a las muestras que contengan
alguna interferencia. Debe prevenirse.
Si se utiliza un procedimiento de medida adecuadamente
calibrado y permanentemente controlado, los resultados
están libres de error sistemático.

27. TIPOS DE ERROR SISTEMÁTICO
valores verdaderos
valoresobservados
constante
proporcional

28. ERROR ALEATORIO (EA) y CCI
Se define para resultados del control de calidad,
como cualquier desviación positiva o negativa
alejada de la media calculada.
Error originado por causas aleatorias o fortuitas y
probablemente no corregibles
Concepto relacionado en forma directa:
imprecisión.
100*
x
s
CV 

29. ERROR ALEATORIO y CCI
Burbujas en los reactivos, tuberías
Inadecuada mezcla de reactivos
Temperatura de incubación inestable
Energía eléctrica inestable
Variaciones operativas en el pipeteo
Las posibles causas de un error
aleatorio puede incluir:

30. ERROR ALEATORIO Y CCI
Expresable en: unidades de la magnitud de la
medida.
Concepto relacionado en forma directa:
imprecisión.
Estimación cuantitativa: desviación estándar,
Coeficiente de variación (CV.)
Aplicables: un grupo de medidas, un
procedimiento de medidas, un instrumento.

32. Control de Calidad: Gráfico de Levey-Jennings
Expresión:
NL
Nº de DS a
obs evaluar

33. Reglas de Westgard para 2 ó 4
controles

34. Reglas de Westgard para 3 ó 6
controles

35. Reglas de Westgard

36. Reglas de Westgard

37. REGLASDE
WESTGARD
12s en el
nivel
10x entre
niveles
R4s entre
niveles
12s en el
nivel

38. EJEMPLO DE APLICACIÓN GRÁFICA LEVEY-JENNYNGS

39. ANALISIS DE POSIBLES CAUSAS
Calibración / Recalibración inexacta
Mezcla inadecuada de muestras con reactivo
Inestabilidad de la fuente eléctrica.
Micropipetas sin verificación
MEDIDAS CORRECTIVAS
Realizar calibración durante periodos más breves
Mantención de equipo e instrumentos revisar calendario de
mantención preventiva.
Adquirir una UPS

41. Control de Calidad Externo GP 1.4 – APL 1.4
OBLIGATORIA GP 1.4
APL 1.4
RG participación CCE
RG análisis y mejora
insatisfactoriedad

43. Ensayos de Aptitud mediante Comparaciones
Interlaboratorio NCh2445.Of1999
PARÁMETRO ESTADÍSTICO PARA EVALUAR DESEMPEÑO
 )
r
r
s
xx
z


Puntaje Z: Z <= 3 Satisfactorio
2>Z<3= Cuestionable
Z > 3= Insatisfactorio
Puntaje Z (z-score)
El z-score compara el error estimado en el resultado con respecto a la desviación
estándar obtenida del análisis en estudio.
ISO/IEC CD 17043.
r = robusta

44. Cuestionable

45. n
Zi
SRZ
n
1i

 
TORIOINSATISFAC3.1SRZ

46. 1.65CV%SESGOET 
Control de Calidad Externo
Competencia Analítica
Error Total

48. ERROR TOTAL (Competencia)
En Términos de Error Total permitido:
Probabilidad (%) Unidireccional z
- Score
Bidireccional
Z- Score
99 2,33 2,58
98 2,05 2,33
97 1,88 2,17
96 1,75 2,05
95 1,65 1,96
90 1,28 1,65
85 1,04 1,44
 ) 100*
x
xx
Sesgode%
r
ri 

ImprecisiónInexactitud
1.65%CV%SESGOET 

50. REQUISITOS DE CALIDAD ANALÍTICOS
PARA IgG, IgM, IgA, IgE, C3, C4 y PCR
LNRI - ISP - CHILE
Analitos SEQC CLIA Alemania ISP
IgG ± 12,0 ± 25 ± 20 ± 22
IgM ± 25,2 VC ± 3 DE ± 28 ± 27
IgA ± 20,3 VC ± 3 DE ± 24 ± 24
IgE VC ± 3 DE ± 37
C3 VC ± 3 DE ± 32
C4 VC ± 3 DE ± 31
PCR ± 68,3 ± 27 ± 49
ETa
± 12,6
± 16,0

51. NIVEL 1 NIVEL 2
N 18 18
82.4 180.7
5.1 8.2
CV 6.2 4.5
X
DE
¿ COMO OBTENER EL %CV ?
Nivel de decisión médica: 150 mg/dL
“Dependerá por lo tanto exclusivamente del analito
que estemos midiendo”…

52. PERIODO % SESGO - %BIAS
MENSUAL 2.61
PROGRAMA DE EVALUACIÓN EXTERNO DE LA CALIDAD
¿CÓMO OBTENER EL % SESGO?
100*
x
x-x
%Sesgo
r
r









Donde:
x = Valor informado
= Valor consenso, media robusta
Entonces si;
X = 157.0 %Sesgo = 2.61
µ = 153.0
X

53. %CV*1.65%SESGOET 
4.5*1.652.61ET 
25%ETaCLIA :
10.0%ET 
ERROR TOTAL TRIGLICERIDOS
¿SOMOS COMPETENTES?
(Control Externo)
(Control Interno)
ENTONCES EL ERROR TOTAL ES:

54. Control de Calidad Externo
Desempeño Analítico
Error Total
Cartas OPSpecs

55. CARTA O GRÁFICA DE ESPECIFICACIONES
OPERATIVAS
OPSpecs Chart, Operational process specifications chart
Describen la imprecisión e inexactitud que son
permitidas para un método y el control de
calidad estadístico necesario para monitorear
y asegurar el cumplimiento de los requisitos
de calidad analítica y/o clínica de una prueba
de laboratorio.
PLANIFICACIÓN!!!

57. SDI – IDE - Puntaje-Z%sesgo - %BIAS - DRP
SRZ (promedio últimos 6 Puntaje-Z, últimas muestras)
n
Zi
SRZ
n
1i

 
SRZ
 )
S
X-X ) 100*
X
X-X
Criterios de Evaluación
Programas de Evaluación externa

59. CUAL ES LA MECÁNICA ACTUAL DE
DESARROLLO EN UN LABORATORIO CLÍNICO

60. Como se utiliza ?
• Se trabaja en la incorporación de datos al software.
• Se deben Implementar las reglas de control de
calidad interna.
• Se aplican de los métodos para fijar los datos.
SOFTWARE CCI MEDLADQC

61. 1. Instalación del software
2. Ingresar el nombre o iniciales del operador
3. Ingresar los analitos a controlar
4. Ingresar el material de control de calidad
5. Asignación de los valores del control de
calidad
6. Ingreso de los valores al control de calidad
7. Implementación de las reglas de Westgard
8. Métodos de fijar los límites en el control de
calidad
Pasos

62. • Ingresar las iniciales del operador.
• Luego la tecla enter.
ENTRADA DEL OPERADOR

63. INGRESO DE ANALITOS

64. • Cada vez que se quiera ingresar un analito nuevo,
seguir las indicaciones anteriores.
– Nombre
– Niveles de control de calidad (1-2-3)
– Unidad de medida
– Decimales a trabajar
– Tecla enter
INGRESO DE NUEVOS ANALITOS

65. INGRESO DE CONTROL (datos)

66. • Cuando
aparezcan el
material de
referencia, se
debe revisar
el “material
usado por”, y
poner enter
ANALITOS Y MATERIAL DE REFERENCIA

67. • Hacer enter en el analito para
asignar el lote a utilizar
• Enter en asignación de lotes
ANALITOS EN QUE ESTÁN INCORPORADOS EL MATERIAL
DE REFERENCIA

68. • Seleccionar el material control
• Hacer “enter” donde corresponda el control
ASIGNACIÓN DEL MATERIAL CONTROL

69. • “mobile limits”
• “fixes limits”
• “lock limits”
FIJAR LÍMITES EN EL GRÁFICO DE
CONTROL DE CALIDAD

70. LÍMITES EN LA GRÁFICA DE
CONTROL DE CALIDAD
 Mob
Lock
Fix 

71. • Método un poco más dificultoso
• Con cada punto que se mide, calcula la
media, la DS y el CV, por lo tanto se cambian
los límites.
• Puede llegar a ser más preciso
• Se utiliza en el período de validación
• Se pone en práctica cuando los valores del
control son desconocidos o se quiere validar
el n=20
Límites móviles

72. • Se realiza después de un período
preliminar de aprox. 20 ó 30 días
• Cada nuevo punto no influirá en la
variación de la media ni de los límites
• La media, DS y CV, pueden seguir
cambiando
“lock limits” (cierre de límites)

73. “lock limits”

74. “lock limits”
 Enter en control
limits

75. • No es un modo estadístico de control de calidad.
• Sólo utilizado por el MedlabQC
• Se deben ingresar los parámetros
– Objetivos
– Desviación permitida
– Desviación en relación al analito y el inserto
• Para analitos con una variabilidad biológica elevada
• Controlar métodos diferentes para el mismo analito
“fixed limits” (fijar límites)

76. INGRESAR LOS PRIMEROS VALORES DE
CONTROL DE CALIDAD
 Fierro :
31,1 / 8,3
29,8 / 8,8
30,0 / 8,1
32,0 / 7,9
31,6 / 8,0

77. Validación de los puntos

78. Ingreso de valores de control de
calidad

79. Ingreso de nuevos valores
Nuevos
valores
38,7 / 4,1

80. • 1 2S un valor +/- 2 DS
• 1 3s un valor +/- 3 DS
• 2 2s dos valores consecutivos +/- 2SD
• R 4s dos valores consecutivos que tienen
una diferencia de 4SD
• 4 1s cuatro valores consecutivos sobre o
bajo la media
• 10x diez valores consecutivos sobre o
bajo la media
REGLAS DE WESTGARD